关键字 非比较;查找;排序;时间复杂度;计数;整数
1 算法的基本思想
通常的排序算法在空间和时间复杂度一定的情况下的时间开销主要是关键字之间的比较和记录的移动。基于计数排序的查找算法(Count-Search)的实现在整个过程无需进行数据的比较,算法的时间复杂度为O( 2*N )。该算法的基本原理是:
根据无符号整数的大小可以和数组元素的下标对应的原则,在程序中可以用整数数组来储存元素的大小关系。对于一个大小为N的整型数组a[],对于每一个元素x,用数组中的元素a[x]记录下小于等于它的元素个数,当要找的是集合中第K个大的元素时,则只需找到该数组中第N-K+1小的元素。即只需要找到该数组中第一个大于或等于 N-K+1的元素,该元素的下标即为第K大的数。
该算法具体可以描述为:假设n个输入元素的每一个都是介于0到M之间的整数,此处M为某个无符号整数。
(1) 对于每一个输入的元素X,首先确定出等于X的元素个数。
(2) 对于每一个元素X,确定小于等于X的元素个数。
(3) 从数组首地址出发顺序查找到第一个小于等于K的元素,则该元素X即为所要查找的第K小的数,顺序查找到第一个小于等于N-K+1的元素,则该元素X即为所要查找的第K大的数。
2 计数查找算法的C语言实现(Count—Search)
2.1 数据结构的设计与程序
假定输入的数组为整型数组A[1..N],length[A]=N,数组中元素最大值为M,数组C[]记录整数元素的大小关系。
Count-Search(int* A,int K)
memest(C,0)//C[0..M]==0初始化C[]
for j=1 to length[A]
do C[A[j]]=C[A[j]]+1
//C[i]包含等于i的元素个数
for i=1 to M
begin
do C[i] = C[i]+C[i-1] //C[i]包含小于等于i的元素个数
if( C[i]>= N-K+1 ) break;//寻找到第N-K+1的元素,即为第K大的元素
end
2.2 算法步骤分析
第一步:第一行的初始化操作之后,在2-3行检查每一个输入元素。如果一个输入元素的值为i,即C[i]的值加1 。于是在第3行之后,C[i]中存放了等于i的元素个数(整数i=0,1,…M)。
第二步:在第4-8之后,C[i]存放了小于等于i的元素的个数。最后从数组C的首地址出发顺序查找第一个使得C[i]>=N-K+1的元素,则第K大的元素即为i 。
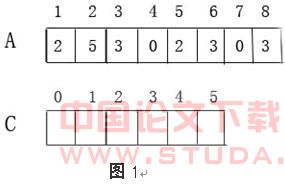
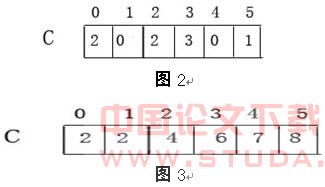
下图给出了Count-Search的运算过程:图1表示初始数组A,C。图2表示运行完程序 2-3行,数组C中的元素C[i]存放的是数组A中等于i的元素个数。图3表示运行4-8行的结果,C中元素C[i]存放的是数组A中小于等于i的元素个数。例如查找该数组第3大的数,则由于C[2]=4>=3,故元素2即为所要查找的第3大的数。
2.3 时间复杂度分析
程序2-3行时间复杂度为O(N),第4-8行时间复杂度为O(M),该算法的时间复杂度为T(n)= O( N+M)。如果数组A[]的最大值M与N成线形关系,即M=O(n),则其时间复杂度为T(n) = O( 2N)。
3 Count-Search算法与Divide-Select算法的比较
Divide-Select 的基本思想是:通过在线性的时间内找到一个划分基准,使得按这个基准所划分出的两个子数组的长度都至少为原数组的ξ倍(0<ξ<1是某个正常数),然后对子数组递归的调用Divide-Select算法,这样就可以在线性的时间内完成查找任务。[6]
该算法得时间复杂度为O(6.09*N)[5],与Count-Search算法相比较可知:Count-Search算法具有更好的时间复杂度。
4 算法测试与比较
为了证实上述结论,在ACER TravelMate 2420 (PM730,512M内存,80G硬盘),Windows XP 平台上编写了三种查找算法的子程序,进行了相应的实验测定,其结果如表1 所示。(实验数据全部采用均分布的无符号整型随机数)
表1
|
数据规模
|
2*10^5
|
8*10^5
|
10^6
|
2*10^6
|
8*10^6
|
10^7
|
8*10^7
|
|
快速排序的查找(qsort)
|
63
|
219
|
265
|
579
|
2203
|
2766
|
62437
|
|
Divide- Select
|
31
|
109
|
140
|
329
|
1157
|
1347
|
11732
|
|
Count-Search
|
15
|
16
|
31
|
31
|
187
|
203
|
1344
|
注:以上时间单位为毫秒MS。
根据以上数据我们可以绘制出数据规模和时间的函数图像。
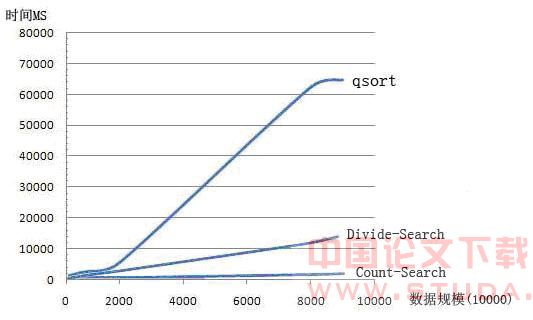
观察分析以上实验结果,可以看出:基于快速排序的查找算法和其他算法相比较具有较差的效率;而采用了分治策略的Divide- Select查找算法的效率可以是基于快速排序的查找算法的几十倍,其时间复杂度在图中也反映为线性。而基于计数排序的查找算法(Count- Search)的时间复杂度同样达到了线性,但是效率却比Divide-Select更高,通过上述实验可以得知:在进行无符号整数查找时,基于计数排序的查找算法(Count-Search)在时间上是最优的。
5 Count-Search的应用范围
在查找无符号整数集合时,应用Count-Search算法,能够降低查找时间复杂度。但是应用Count-Search算法时要注意:该算法只适用于整数的查找,且查找集合S的最大值M与S中元素个数N不成指数关系,即M 不能远大于N。因为当M过大时,首先内存开销就会很大,其次时间复杂度也会相应的提高。
该算法充分的运用了整数的特性,整个运算过程中无需数据的比较和交换,大大降低了算法的时间复杂度,因此该算法可以在工程统计中得到大规模运用。例如:随着网络的发展和应用,网络中的信息量成倍的扩大,而在其中我们关注的最多的则是统计排名比较靠前的信息,如果将全部过亿的统计量排序,则由于数据量过大,则会浪费大量的时间和资源。而采用Count-Search的查找算法,就可在线性的时间完成。
6 结束语
本文中提出的一种基于计数排序算法的整数查找算法,该算法在运算过程中无需进行数据的比较和交换,该算法可以应用到大规模的整数查找,算法的时间复杂度很低,而且避免的大量的数据比较和交换,同时在时间上是最优的。
参考文献
[1]崔泽鹏,李伟生. EREW PRAM模型上指数级分割待处理数据集的并行多选算法[J].北方交通大学学报,2003,(2):46-49
[2]班志杰,高光来. 一种Byte查找第K个元素的算法研究[J]. 内蒙古大学学报,2004,(3):322-324
[3]Thomas H.Cormen Charles E.Leiserson. 《算法导论》[M]. 北京:机械工业出版社。2006.9:98-99
[4]Muhammad H.Alsuwaiyel. An optimal parallel algorithm for the multiselection problem[J]. Parallel Computing,2001,(27):861—865
[5]江华. 求第K个元素的快速排序算法[J]. 韶关学院报,2003,(6):32-34
[6]王晓东.《算法设计与分析》[M] .北京:清华大学出版社,2003.1:39-43





